在对复杂构造进行偏移成像时，傅立叶有限差分(FFD)法是目前为止公认的单程波方法之一。对于三维情形，常用的双向分裂FFD法虽然有很高的执行效率，但同时也引入了很大的分裂误差，极大地影响了对角线方向的成像精度。为了消除分裂误差，以往的方法主要基于频率空间域或者频率波数域进行。这些只在单一域中进行的方法存在计算量庞大，或者不能很好的适应剧烈的横向速度变化，因而很难在保持计算效率的前提下提高陡倾角构造的成像精度。

地质与地球物理研究所地球深部结构与过程研究室的张金海副研究员和姚振兴研究员发展了一种在双域中交替进行分裂误差修正的新方法。该方法能够很好地适应强横向速度变化介质中的陡倾角成像问题，而且其计算量的增长仅为常规双向分裂FFD法的三分之一左右，较好地保持了FFD法的执行效率。众所周知，FFD法是有限差分法和傅立叶法两大类方法的有机结合，它是上世纪末发展的最有效的单程波方法之一。本研究的贡献在于进一步加深了有限差分法和傅立叶法的融合，采用高阶傅立叶修正来减少分裂误差的影响，得到了较好的实验效果。研究还通过全局优化手段大幅度地提高了三维算子的整体精度，使各个方位角的精确传播角度均大于60度，较未修正前的35度有明显提升。

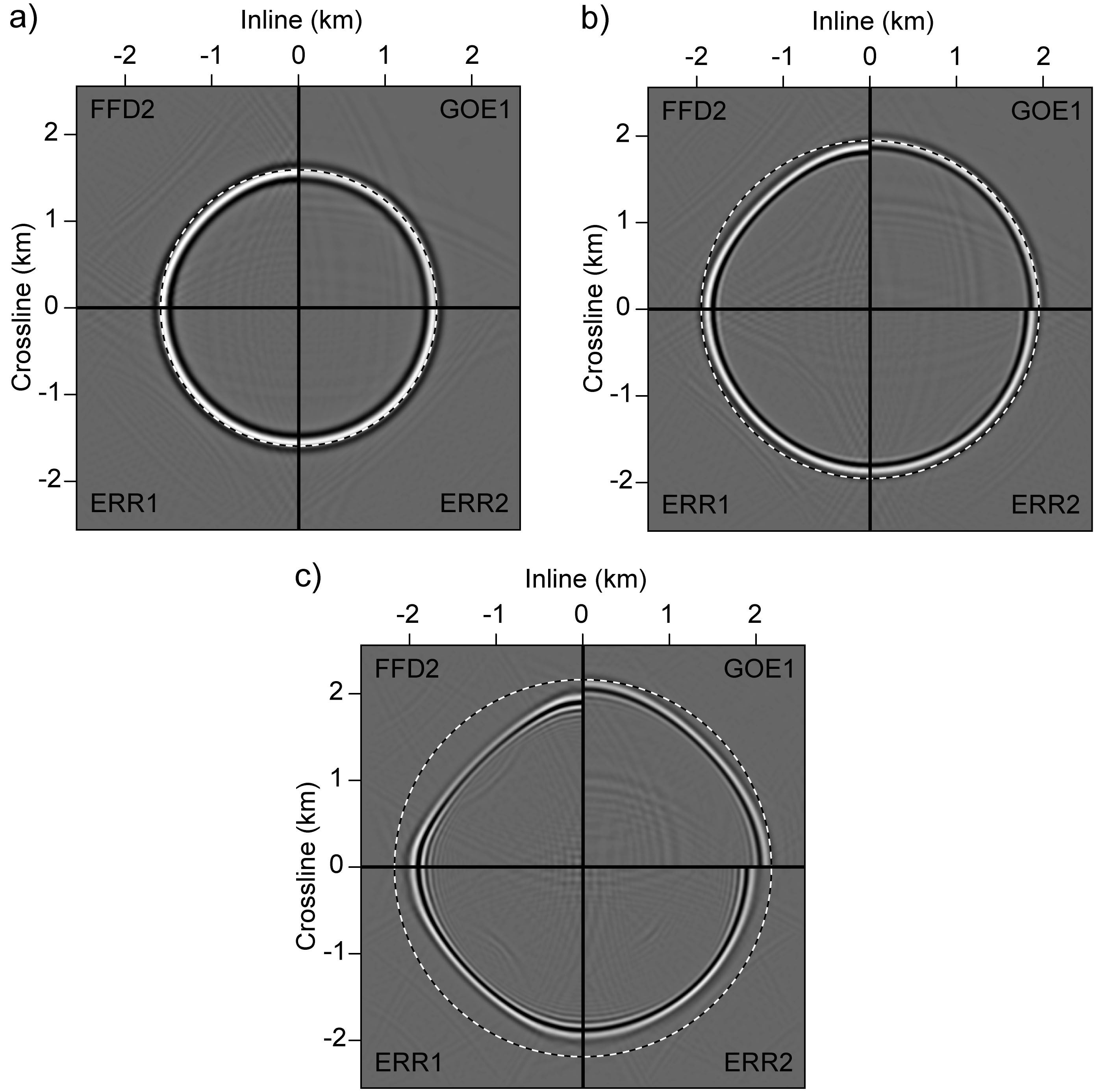
附图说明：不同地层倾角处的三维脉冲响应的切片对比图。（a）45度倾角;（b）60度倾角;（c）75度倾角。每幅图中均包含四个部分，每一部分都由不同的方法得到。其中FFD2代表常规的双向分裂FFD法，ERR1代表只采用一个修正项的未优化方法，ERR2代表采用两个修正项的未优化方法，GOE1代表只采用一个修正项的全局优化方法。不难看出，同虚线标出的理论位置相比较，带有一个修正项的全局优化方法具有最高的精确传播角度。

该研究成果近期发表在勘探地球物理领域的国际权威期刊Geophysics上(Zhang and Yao. Reducing two-way splitting error of FFD method in dual domains. Geophysics, 2011, 76, S165-S175)。

原文链接