地震波正演模拟是逆时偏移（Inverse time migration，RTM）和全波形反演（Full-waveform inversion, FWI）的基础，在地震数据处理过程中起着关键作用。与传统的时间域方法相比，频率域方法具有适合多炮计算、便于模拟粘滞效应、易于并行运算等优点。频率域弹性波正演模拟中的传统9点方法（图1a）适用于任意不等的空间采样间隔，具有很强的灵活性，但需要很细的网格划分才能达到较高的模拟精度。由于求解亥母霍兹方程的内存需求并非简单的线性增长，细网格意味着计算成本的大幅上升。前人将笛卡尔坐标系进行45°旋转，开发了旋转优化9点方法（图1b），相对传统9点方法具有更高的精度，有效地节省了计算成本。然而，该方法的一个缺陷是其限制了所有方向上的采样间隔必须相等，这就可能导致在一些稀疏采样即可满足精度要求的方向上仍必须进行密集采样，使得其灵活性不如传统9点方法。 

图1 （a）传统9点方法：θ角没有限制，但数值精度低，需要很高的计算成本才能满足精度要求；（b）旋转优化9点方法：数值精度高，但θ角必须为45°，在一些稀疏采样就能满足精度要求的方向上必须进行密集采样；（c）仿射优化9点方法：数值精度更高，且θ角没有限制，在节省计算资源上具有更多的灵活性

　　为解决上述问题，中科院地质与地球物理研究所油气资源研究院重点实验室董树立博士及其导师陈景波研究员提出了仿射坐标变换法（如图1c）。与笛卡尔坐标系不同，仿射坐标系不必约束坐标轴彼此正交。他们基于仿射坐标变换提出的优化9点方法同时克服了传统9点方法的低精度问题以及旋转优化9点方法的等采样间隔的限制。此外，他们还将这种仿射技术应用于对自由表面边界的处理。由于介质内部和自由表面在表达式上的高度一致性，使得二者可共享一套优化系数，同时提高了体波和面波的模拟精度。Overthrust模型数值算例表明，仿射优化方法能以更粗的空间采样网格（意味着更低的计算成本）提供高精度的计算结果（如图2所示）。这种仿射优化方法尤其适用于一些纵、横向速度不相等勘探区域和理论速度模型。 

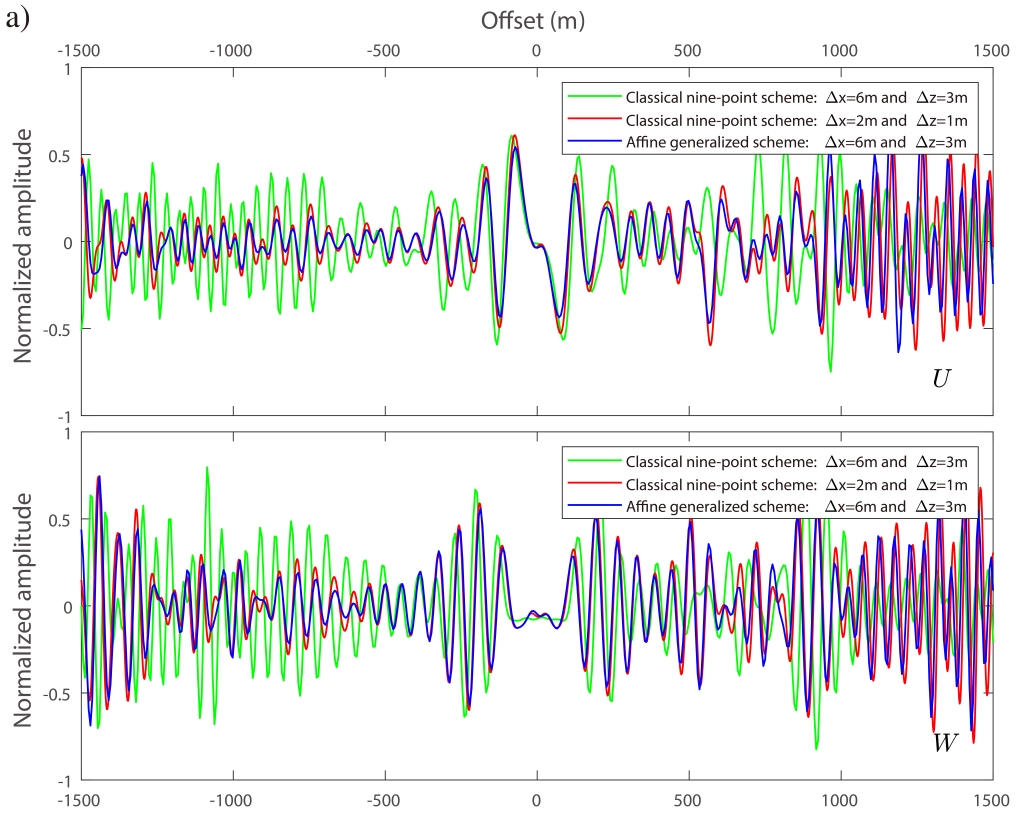
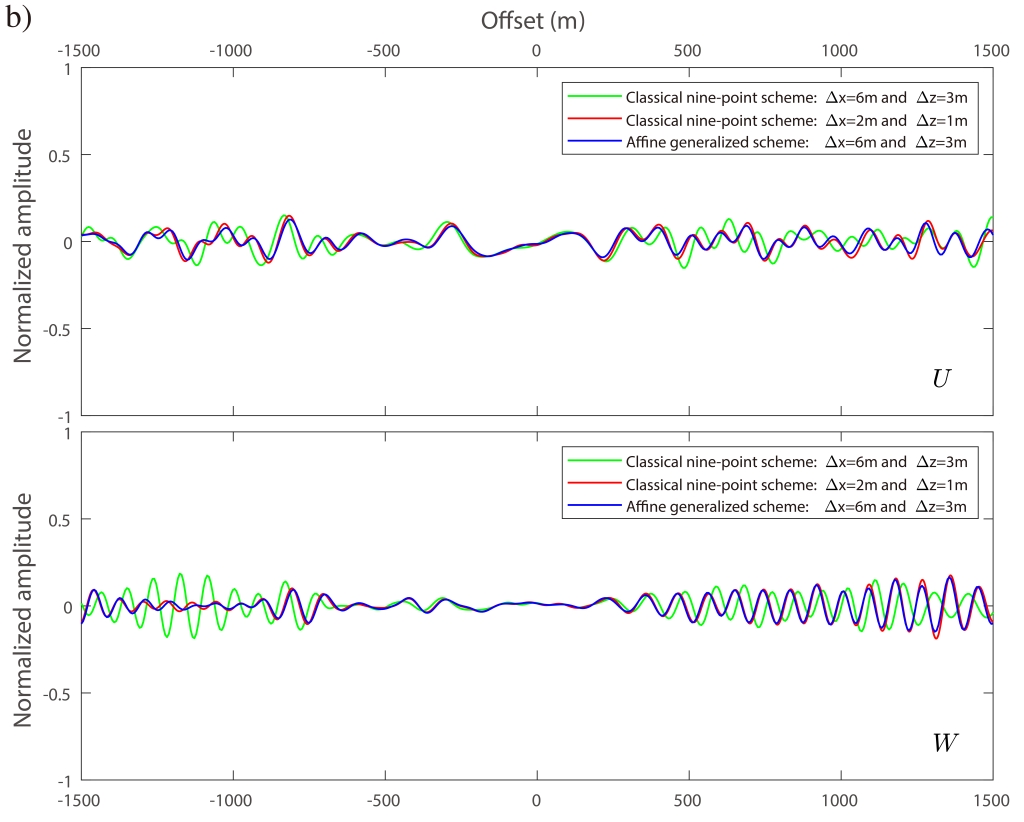
图2 复杂介质下，传统方法与仿射优化方法在（a）自由表面处，（b）介质内部的频率域地震图。仿射优化方法能以更粗的空间采样网格提供高精度的结果　　  

　　研究成果发表于国际学术期刊Geophysics（董树立，陈景波^*. An affine generalized optimal scheme with improved free-surface expression using adaptive strategy for frequency-domain elastic wave equation [J]. Geophysics, 2022, 87(3): T183-T204. DOI: 10.1190/geo2021-0345.1）。研究受国家自然科学基金项目（42074159 & 41874163）资助。