有限差分法算法简单直观，广泛应用于地震波数值模拟，然而该方法在高频率和粗网格情况下会产生较强的空间数值频散假象。常系数优化方法可以在保持计算效率的前提下有效地压制空间数值频散，但以往的优化方法会导致低波数区间出现较大误差，特别是导致长时程模拟累积误差明显，从而影响深层反射波的模拟精度。 

　　中科院地质与地球物理所地球与行星物理院重点实验室博士生苗中正与导师张金海研究员，提出了一种基于L₁范数优化有限差分常系数的新方法。首先，他们基于空间频散关系利用L₁范数构建目标函数；然后，将其离散并转化为受限L₁范数最小化问题；最后，使用交替方向乘子法求解该问题。 

　　以8阶有限差分方法为例，图1对比了各种方法的二维波数响应误差，图2进一步给出了特定角度下的误差曲线。可以看出，新方法在低波数区间和中波数区间具有最小的误差。 

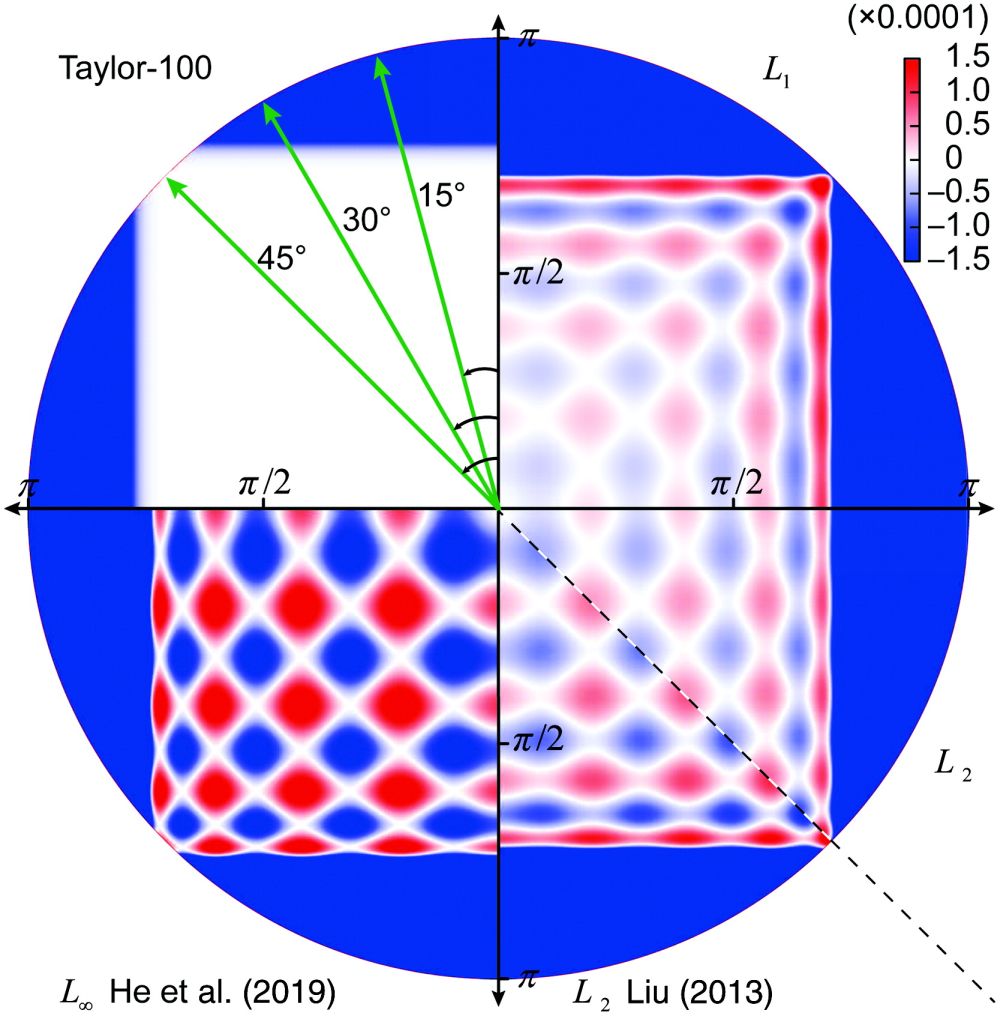
图1 优化有限差分系数的二维波数响应误差对比图

图2 不同角度下的响应误差曲线对比

　　图3所示的波场及误差快照表明，在相同的误差限或相同的有效带宽条件下，新方法的总体性能要优于其他方法，尤其是在长时程模拟中，这对于深部目标的反演和偏移成像具有实际意义。 

图3 不同时刻（T=1，5，10秒）的波场快照及误差

　　研究成果发表于Geophysics。(Miao Z and Zhang J. Reducing error accumulation of optimized finite-difference scheme using the minimum norm[J]. Geophysics, 2020, 85(5): T275–T291. DOI: 10.1190/geo2019-0758.1)（原文链接）