科学数值计算是20世纪中最重要的科学进步之一。科学计算在生命科学、医学、经济学、物理学、化学和地球科学等诸多领域形成了分支性学科，比如地球科学领域中包括计算地震学、计算地球化学，地球动力学模拟等等。其中计算地震学在地球内部结构研究中发挥了极为重要的作用，地震波传播的数值模拟是其重要的研究方向。 

中科院地质地球所地球深部结构与过程研究室孙伟家副研究员及其合作者发展了基于交错网格卷积算子的高精度弹性波模拟方法。他们利用该方法模拟了地震波在地球介质中的传播，并识别了多种地震相。该方法是一种半解析半数值方法，利用反傅里叶变换解析表达一阶空间偏导数，具有与解析解相近的计算精度和经典有限差分方法相同的计算效率。通过对比发现，该方法8阶算子的计算精度与经典交错网格有限差分16阶算子相当(算子阶数越高，计算精度越高)，但计算效率提高了一倍。 

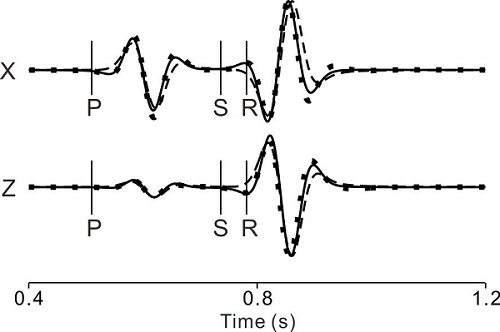
图1 该方法不同离散网格间距(大网格和小网格分别用虚线和点线表示)时计算的地震波形与解析解(实线)的比较。X和Z分别代表地震波场的水平分量和垂直分量，P, S, R分别代表P波、S波和Rayleigh波的到时

图2 该方法8阶算子长度(黑线)和经典交错网格有限差分方法16阶算子长度(红线)合成的理论地震图。上图为水平分量，下图为垂直分量。图中蓝色虚线给出了相应地震相(Pn, Pg, PmP, Sn, Sg, Rg, PgPg)的参考到时

由于获取精细的地球内部速度结构需要很大的计算成本，该方法兼具高计算精度和高计算效率的优势，其将为进一步反演地壳和上地幔的精细速度结构奠定坚实的基础和提供有力的计算保证。 

     以上研究成果近期发表在国际知名期刊Journal of Computational Physics上(Sun et al. A staggered-grid convolutional differentiator for elastic wave modelling, Journal of Computational Physics, 2015, 301: 59-76)。

原文链接