基于全波形反演(FWI)以及精确的三维全球地震模型谱元法(SEM)(Komatitsch and Tromp, 2002)波场模拟方法,全球地震层析成像技术在近四十年取得了显著的进展。然而,要实现更高分辨率的成像,仍然面临着两大挑战。一方面,更短周期地震波的SEM全球正演模拟成本高昂,与最小周期的四次方成正比(Lyu et al., 2020);另一方面,全球地震和台站的分布极为不均,这一现状在短时间内难以改变。不过,对于地震数据覆盖相对较好的某些地球深部区域,比如位于核幔边界上方冰岛、夏威夷等地幔柱的的根部区域(如图1概念图),地震学家则有望获取更高分辨率的地震成像结果,用以辅助理解地球动力学中地幔柱起源等基本问题。
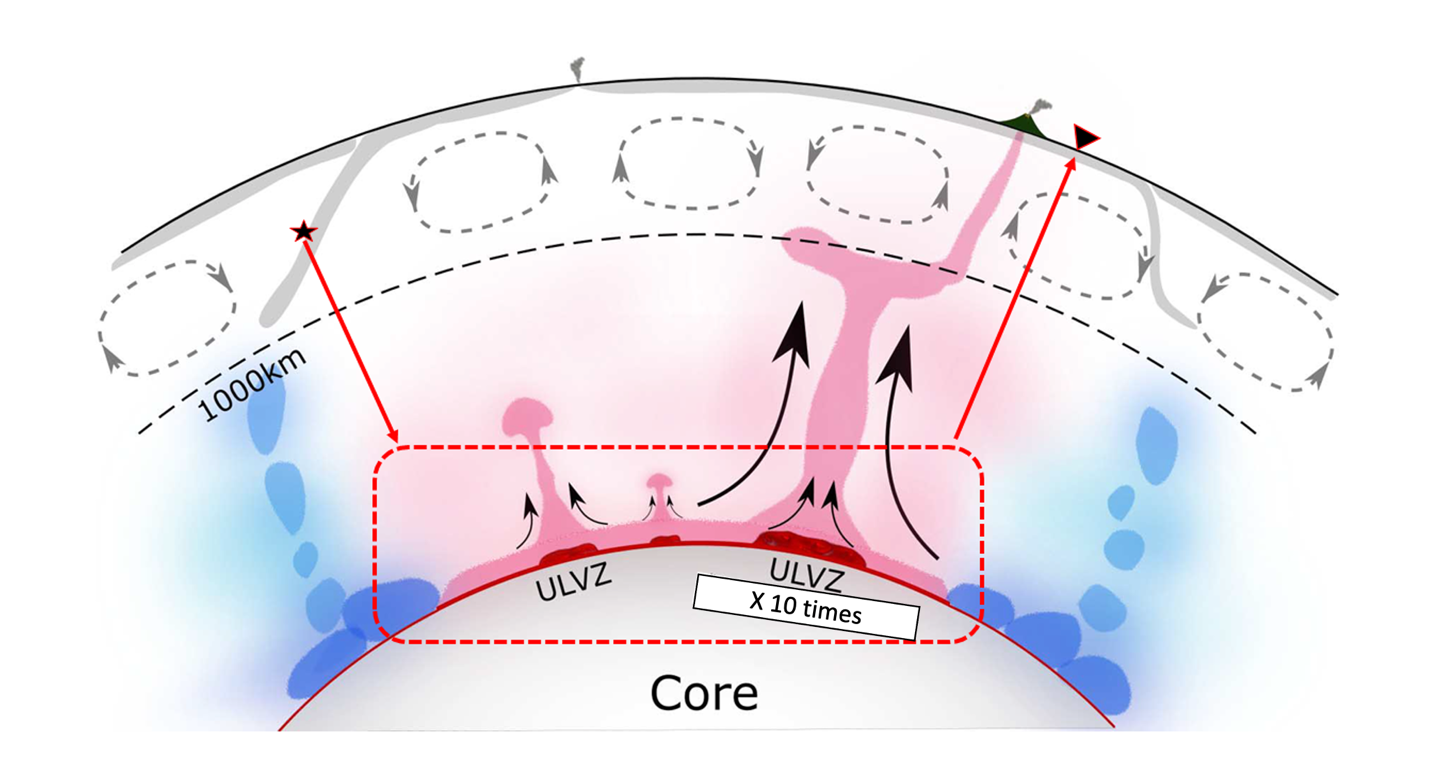
图1 利用远端分布的震源和台站,基于“子域波形层析成像”(BoxTomo)探测核幔边界的超低速体(ULVZ)(修改自Yuan and Romanowicz, 2017)
将FWI应用到埋藏于地球深部的小尺度速度结构成像时,与探索的目标结构的尺度相比,往往需要计算超远距离的地震波场数值模拟。“子域波形层析成像”(简称为“BoxTomo”)(Masson et al., 2017)被认为是下一代地球内部多尺度结构成像的重要发展方向之一。该方法选择在特定区域内部成像,基于地震波混合数值模拟,将波场计算分解为三个部分,包括远震源端和远台站端到子区域边界的全球尺度地震波数值模拟,以及子区域内部的数值模拟。其中只有子区域内部需要在每次模型更新时进行波场模拟,从而可以极大地节省计算时间(Adourian et al., 2023)。
为了在包含固液耦合边界且远离震源和台站的子区域内部应用BoxTomo方法(图一),难点在于需要逐步实现:1)在远震源端进行全局数值模拟时,设计输出远震对应的固液等效震源;2)在局部数值模拟时,通过混合数值模拟与固液耦合的结合,将地震波场模拟限制在跨越固液耦合边界的子区域内;3)在远台站端进行全局数值模拟时,设计输出后续卷积所需的格林函数;4)稳定的、有效的固液耦合吸收边界的实现等。针对这些难点问题,加州大学伯克利分校、中国科学院地质与地球物理研究所和法国波城大学的研究人员进行了合作,在弹性波和声波表示定理的约束下(Masson et al., 2014; Lyu et al., 2022),提出了一个适用于固液耦合模型的地震波混合数值模拟方法(Hybrid Solid-Fluid Coupling, HSFC)。该方法首先统一了用于求解二维/三维声波方程的不同位移势表达式(SPECFEM2D和SPECFEM3D_Globe程序所采用的位移势定义不同),进而提出了一个适用于三维背景模型下地震波固液耦合混合数值模拟的统一框架(详见Lyu et al., 2025中公式10,17,18)。
地震波固液耦合混合数值模拟的核心思想是将波场计算分为全局固液模拟计算和局部固液模拟计算两种。全局计算在已知的参考模型中进行,而局部计算则仅在迭代更新的目标子区域内进行。子区域内的局部计算,依赖子区域边界处输入的等效作用力(震源加载),同时伴随着输出等效作用力的存储(见图2)。这种方法特别适用于震源和台站位于目标区域外部的情况(SORO,Source Outside and Receiver Outside),比如用于台站分部较少的海洋底部、地球深部核幔边界以及内外核边界处的多尺度结构研究。
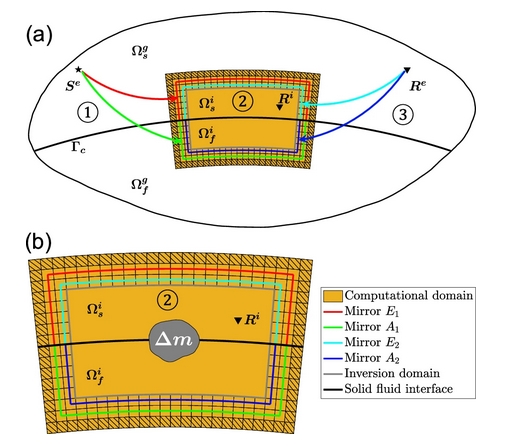
图2 含固液界面的“子域波形层析成像”正演模拟流程:(1)在三维全球地震参考模型中,计算从远震源端到目标子区域边界的波场,计算并存储下固液点集E1/A1处的输入等效作用力;(2)在子区域边界固液点集E1/A1处加载输入等效作用力并进行区域地震波数值模拟,并记录固液点集E2/A2处的输出等效作用力;(3)在三维全球地震参考模型中,计算从远台站端到目标区域边界E2/A2点集处的格林函数。基于地震学的互易定理,E2/A2点集处的输出等效作用力和格林函数的卷积计算可以将波场从子区域边界外推到位于子区域外部的台站
研究团队通过一系列数值实验验证了所提出的HSFC方法的准确性及高效性。对于二维固液耦合混合地震数值模拟,目标子区域设置为核幔边界和海洋底部。构建了三个局部模型:参考模型、包含超低速体的模型和包含起伏核幔边界的模型。实验结果表明,在目标区域内没有散射体时,混合模拟能够准确恢复局部波场,且没有任何散射能量产生(图3a、图3b)。当目标区域内存在散射体时,混合模拟能够准确捕捉到散射波场,且波形误差极小。在核幔边界上方存在超低速体结构的情况下,横波穿过该区域时会产生类似面波的散射波(图3c、图3d)。而该带频散的面波是由核幔边界上方的薄层超低速体异常产生的。相比之下,如果核幔边界呈现起伏,那么散射波的模式会相对简单(图3e、图3f),且类似面波的振幅要小得多,所产生的Scholte波的传播速度小于面波,是由核幔边界的起伏引起的。值得强调的是HSFC的计算效率,在二维模拟中,该方法在保持高精度的同时,显著地减少了计算时间,减少比例与单元个数比例类似。
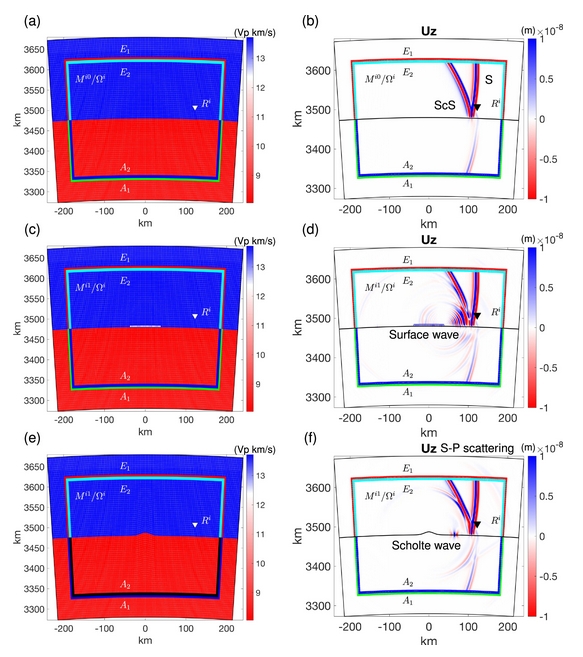
图3 在三个不同的子区域模型中进行了三次二维固液耦合混合数值模拟,这三个模型采用了相同的混合输入作用力,这些力是从全局参考模型在对应点E1和A1处的数值模拟中计算获得并提前存储。子区域的空间尺寸为(7.5°,400 km),在核幔边界(CMB)上下分别延伸了200 km,局部网格由120×(40+40)个单元组成。图(a-f)展示了局部参考模型、超低速体(ULVZ)模型和起伏CMB模型以及相应的波场。ULVZ(白色方块(c)和蓝色网格(d))在CMB上方延伸了5 km,水平宽度为1.25°,其弹性参数变化为剪切波速降低30%,纵波速降低10%,密度增加10%。起伏CMB呈高斯形状,由高度(7.5 km)和水平宽度(0.375°)两个参数定义
在三维HSFC数值试验中,研究团队以全球三维层析成像模型SEMUCB_WM1(French & Romanowicz 2015)作为背景,在核幔边界附近叠加了一个超低速体(图4a),实验结果表明,对于90°震中距、最小周期为15秒的地震波,固液耦合混合模拟能够准确捕捉到散射波场(图4b),且合成的波形误差较小(图5)。主要的散射波形(约1400秒)与Shdiff的后驱震相波形相匹配(图5d),这与实际观测数据中的情况相类似。在空间尺度子域模型中,计算效率实现了约3000倍(SPECFEM3D_Globe: 11857.9 CPU小时,SPECMAT: 4 CPU小时)的提升,凸显了混合固液耦合数值模拟在BoxTomo中的准确性、高效性和应用潜力。

图4 三维地震波固液耦合混合数值模拟的模型及波场。(a) 子区域三维目标模型包含了SEMUCB_WM1模型的下地幔部分,叠加的超低速体(白色区域),以及PREM模型的外核部分。核幔边界用黑点表示;(b) 在1260秒时,观察到相应的Z分量局部散射波场。在固液点集E1(红色)和A1(绿色)上加载了输入等效作用力。在固液点集E2(青色)和A2(蓝色)上计算并存储了用于后续卷积所需的输出等效作用力(局部计算)和对应的格林函数(全局计算)
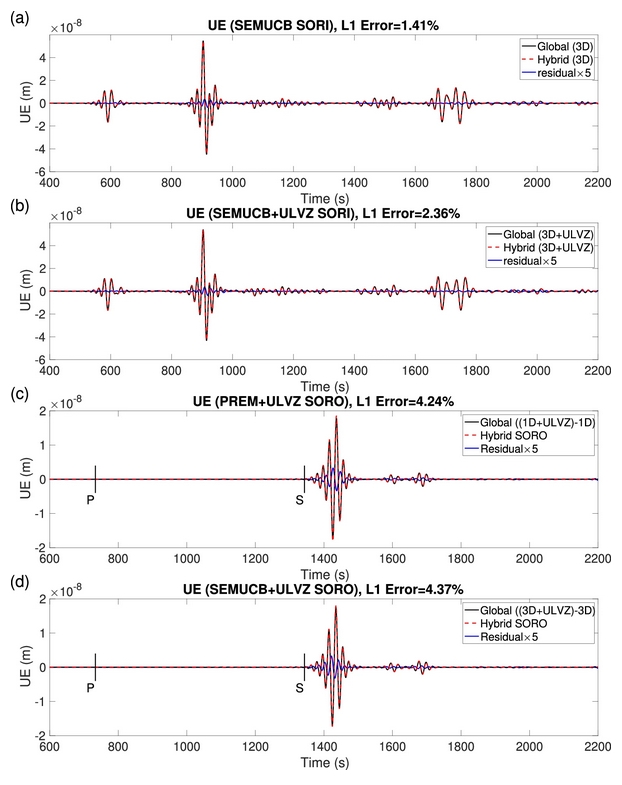
图5 三维地震波固液耦合混合数值模拟所得波形与全局计算波形对比图。(a-b)对应的是震源和台站在区域外部和内部(SORI)的波形对比。对应的模型分别是SEMUCB_WM1和SEMUCB_WM1叠加超低速体(ULVZ)。区域内部的台站为图4a中的黑色三角形。(c-d)对应的是震源和台站均位于子区域外部(SORO)情况下E分量波形对比图,对应的背景模型分别是PREM和SEMUCB_WM1
研究团队对HSFC的数值收敛性,合成理论地震图的完整性,算法的计算效率进行了详细的讨论。尽管BoxTomo 的正演计算效率上取得了显著进展,但在计算短周期(几秒)混合数值模拟时,仍然面临较大的全局计算成本。未来的研究将进一步探索更高效、更灵活的全局数值模拟算法,比如高效的AxiSEM3D(Leng et al., 2019)以及三维全球分布式有限差分法(DFDM)(Masson et al., 2024; Lyu et al., 2024)的开发。此外,子域内部的数值模拟的进一步优化也将是未来研究的重要方向,特别是稳定、高效的固液耦合吸收边界的实现。
该研究提出的地震波固液耦合混合数值模拟方法为在地球内部任意目标区域进行高分辨率地震成像提供了理论基础。通过统一的位移势表达式和高效的固液混合数值模拟框架,研究人员能够在保持计算精度的同时,显著减少计算成本。这一方法的应用前景广阔,特别是在研究海洋底部、核幔边界以及内外核边界处的复杂小尺度结构时,具有重要的科学意义和实际应用价值。
主要参考文献
Adourian S, Lyu C, Masson Y, et al. Combining different 3-D global and regional seismic wave propagation solvers towards box tomography in the deep Earth[J]. Geophysical Journal International, 2023, 232(2): 1340-1356.
French S W, Romanowicz B A. Whole-mantle radially anisotropic shear velocity structure from sgpectral-element waveform tomography[J]. Geophysical Journal International, 2014, 199(3): 1303-1327.
French S W, Romanowicz B A. Whole-mantle radially anisotropic shear velocity structure from spectral-element waveform tomography[J]. Geophysical Journal International, 2014, 199(3): 1303-1327.
Komatitsch D, Tromp J. Spectral-element simulations of global seismic wave propagation—I. Validation[J]. Geophysical Journal International, 2002, 149(2): 390-412.
Leng K, Nissen-Meyer T, Van Driel M, et al. AxiSEM3D: broad-band seismic wavefields in 3-D global earth models with undulating discontinuities[J]. Geophysical Journal International, 2019, 217(3): 2125-2146.
Lyu C, Capdeville Y, Zhao L. Efficiency of the spectral element method with very high polynomial degree to solve the elastic wave equation[J]. Geophysics, 2020, 85(1): T33-T43.
Lyu C, Zhao L, Capdeville Y. Novel hybrid numerical simulation of the wave equation by combining physical and numerical representation theorems and a review of hybrid methodologies[J]. Journal of Geophysical Research: Solid Earth, 2022, 127(5): e2021JB022368.
Lyu C, Masson Y, Romanowicz B, et al. Introduction to the distributional finite difference method for 3D seismic wave propagation and comparison with the spectral element method[J]. Journal of Geophysical Research: Solid Earth, 2024, 129(4): e2023JB027576.
Lyu C, Romanowicz B, Zhao L, et al. Efficient hybrid numerical modeling of the seismic wavefield in the presence of solid-fluid boundaries[J]. Nature Communications, 2025, 16(1): 1722.(原文链接)
Masson Y, Cupillard P, Capdeville Y, et al. On the numerical implementation of time-reversal mirrors for tomographic imaging[J]. Geophysical Journal International, 2014, 196(3): 1580-1599.
Masson Y, Romanowicz B. Box tomography: localized imaging of remote targets buried in an unknown medium, a step forward for understanding key structures in the deep Earth[J]. Geophysical Journal International, 2017, 211(1): 141-163.
Masson Y, Lyu C, Moczo P, et al. 2-D seismic wave propagation using the distributional finite-difference method: further developments and potential for global seismology[J]. Geophysical Journal International, 2024, 237(1): 339-363.
Yuan K, Romanowicz B. Seismic evidence for partial melting at the root of major hot spot plumes[J]. Science, 2017, 357(6349): 393-397.
(撰稿:吕超,赵亮/油气理论与方法学科中心)

