扩散作用是物质内质点运动的基本方式,是重要的传质过程之一,宏观上表现为物质的定向迁移,包括化学扩散(化学浓度梯度驱动)和热扩散(温度梯度驱动),其支配着元素/同位素在物质内的迁移和再分配,广泛存在于矿物、熔体、流体和气体中。在给定的条件下,化学扩散引起的元素丰度变化是时间的单调函数,这正是扩散年代学(Diffusion chronometry)推断地质过程时间尺度的根基。
由于不同元素的扩散速率可存在几个数量级的差异,多元素扩散联用可约束数分钟到数百万年时间尺度的岩浆活动。因此,扩散年代学可提取极高分辨率的时间信息,是研究各类岩浆过程的时长及速率时广泛采用的绝佳途径之一(图1)。
以下,我们结合新加坡南洋理工大学 Fidel Costa教授及其合作者于2020年发表在Nature Reviews Earth & Environment上的综述文章“Diffusion chronometry and the timescales of magmatic processes”,简要介绍扩散年代学在探究岩浆过程时间尺度上的理论基础、应用现状及发展前景。
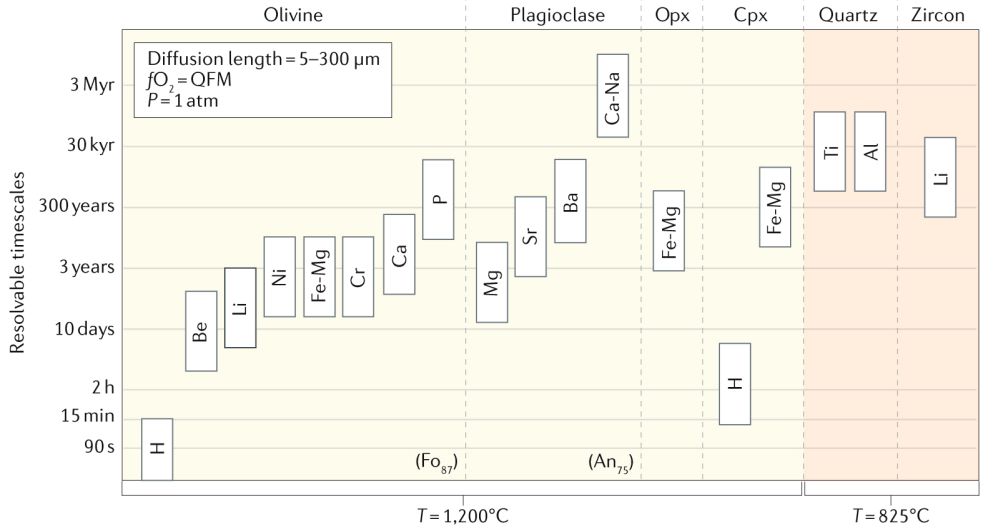
图1 特定条件下,不同元素在常见矿物中的扩散时间尺度分辨范围总结(Costa et al., 2020)。图示时间尺度的估算基于以下参数条件:对于赋存于玄武岩中的矿物(如橄榄石、斜长石、斜方辉石和单斜辉石)和流纹岩中的矿物(石英、锆石),分别取1200℃和825℃为例;假设扩散长度为5-300微米,氧逸度为QFM buffer,压力为1 个标准大气压
一、扩散年代学的研究基础
1.扩散环带的形成
扩散年代学常被用于推断岩浆从存储到喷发的时间尺度。将喷发前岩浆活动的时长与岩浆活动引起的地震、地表形变以及火山排气等观测结合,火山学家可构建岩浆喷发前的运动轨迹,厘清火山喷发机制和规模的主控因素。
以火山下的玄武质岩浆系统为例。上涌岩浆将深部结晶的矿物(如橄榄石)带至浅部岩浆房;在岩浆化学分异和/或岩浆补给的作用下,浅部岩浆房中的岩浆的化学成分发生变化(如向低镁演化);新生长的橄榄石边缘继承这一组成变化,形成具不同元素组成的环带。在化学浓度梯度(化学势)的驱动下,元素在晶体内发生扩散,扩散计时器开始计时。随着岩浆持续分异以及来自深部岩浆的挥发分补给,岩浆中挥发份逐渐达到饱和,岩浆在浮力作用下向浅表运移,最终喷发。岩浆在喷发前快速上移及喷出地表的过程中会经历相对快速的降温,当温度足够低时,晶体中元素的浓度几乎不再变化,扩散计时器停止。通过测量火成岩晶体中元素浓度的空间分布,可以反推出在一定温度下元素在晶体中扩散所消耗的时间(图2)。
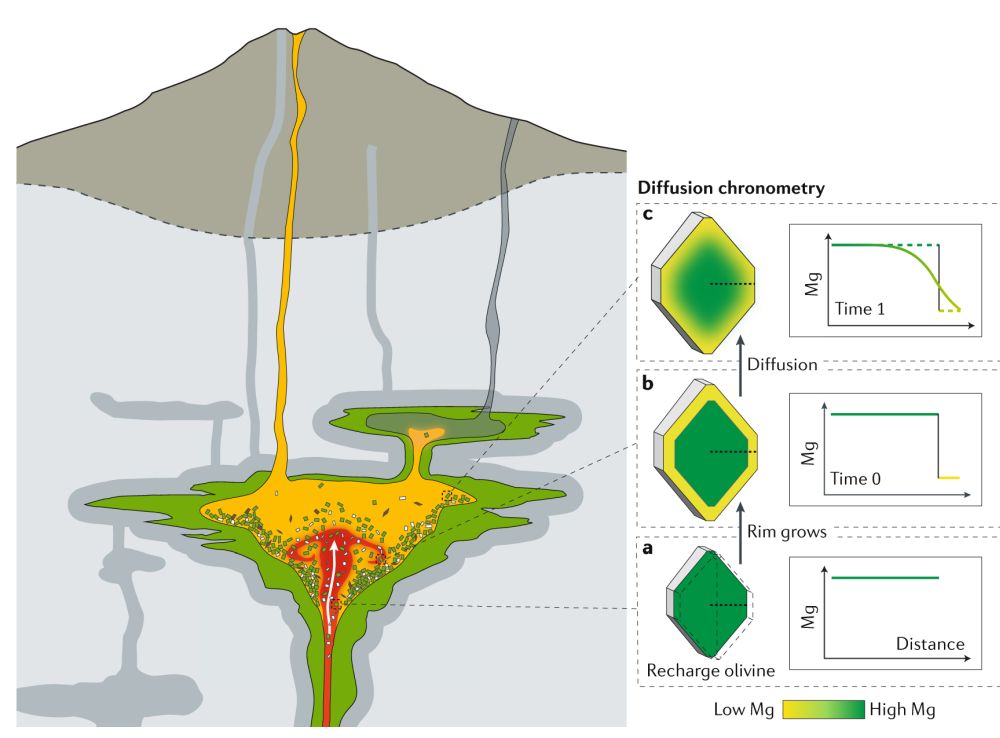
图2 岩浆过程橄榄石中镁元素扩散环带形成示意图(Costa et al., 2020)
2.环带成分的测量
观测自然样品中元素浓度空间分布的分析技术主要包括电子探针(EPMA)、离子探针(SIMS)、红外线光谱(FTIR)、激光剥蚀电感耦合等离子体质谱仪(LA-ICP-MS)等。通常来说,元素浓度剖面越精细(测试精准度和空间分辨率越高),计算获得的扩散时间越精确。例如,利用电子探针获得的浓度剖面的分辨率可以达到1微米左右,而使用NanoSIMS则可以获得空间分辨率高达几十纳米的剖面,从而获得更精确的扩散时间。
3.影响扩散时间的参数及扩散的数值模拟
在观察到晶体中的元素环带之后,我们可以利用各种化学分析仪器,测出元素浓度(C)在晶体中随距离(x)变化的剖面(如图3)。浓度剖面的形态与时间(t)和元素的扩散系数(D)的关系可以用菲克第二定律(Fick’s second law)表示:
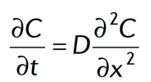
扩散系数(D)通常由特定温度及压力条件下已知时长的扩散实验测得。扩散系数与温度密切相关,通常可以用阿伦尼乌斯(Arrhenius)方程表示:
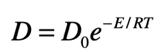
其中,T是温度(单位K),D0 是指前因子(即温度无限大时的扩散系数), E是表观活化能,R是 理想气体常数。
理想气体常数。
由于温度对扩散系数(D)的巨大影响,只有在正确地估算扩散温度的前提下,我们才能获得准确的扩散系数及扩散时间。对扩散温度的计算多基于已有的矿物温度计(Putirka, 2008),但是,如何进一步减小矿物温度计的误差仍是一个难题。除温度之外,一些元素(如橄榄石中的Fe-Mg)的扩散系数(D)还与氧逸度、压力、矿物的化学成分及扩散的各向异性等因素有关。这些参数的误差也会影响估算的扩散时间的误差。
利用已知的扩散系数,以及设定的扩散的初始条件及边界条件,我们可以使用有限差分法对菲克第二定律求解。把有限差分模拟获得的经假定时长扩散后形成的浓度剖面,与自然晶体中测得的浓度剖面进行对比,便可以找出拟合程度最好的曲线,由此获得扩散时长。
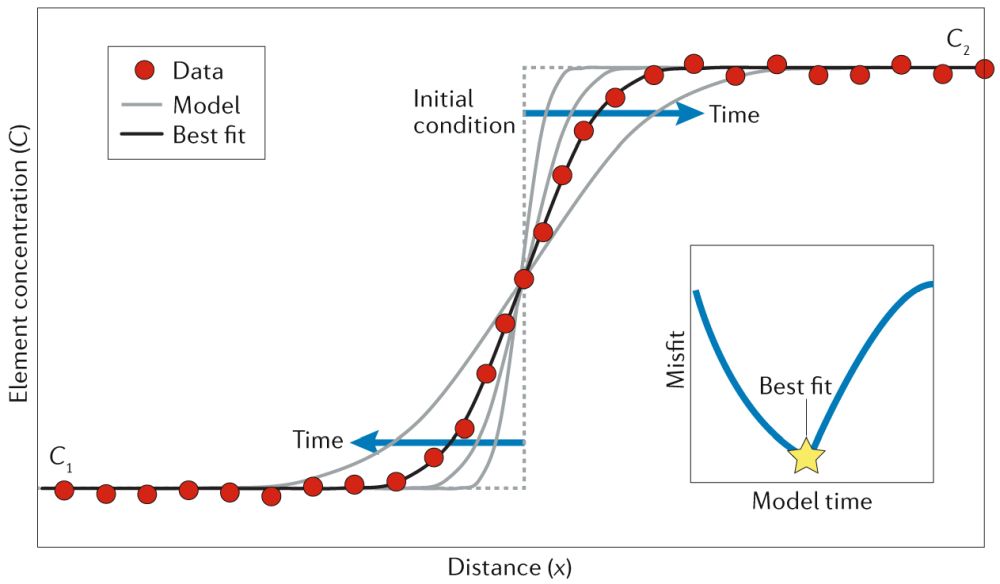
图3 利用特定初始条件对元素浓度剖面进行扩散模拟的示意图(Costa et al., 2020)
针对扩散的有限差分数值模拟可以利用多种编程语言实现。目前已有一些针对特定矿物中特定元素扩散的模拟计算工具,包括针对橄榄石扩散的DIPRA程序(exe)(Girona and Costa, 2013)和针对磷灰石扩散的ApTimer网页计算工具(https://aptimer.wovodat.org ;Li et al., 2020a)。
二、扩散年代学——研究实例
1.岩浆在岩浆房中的滞留时间:‘冷’‘热’储存之争
将前文提到的扩散原理、测量方法以及数值模拟等方法应用在火山岩矿物上,可以估算出岩浆混合后在岩浆房中的滞留时间。喷发前的岩浆滞留时间对偏基性(如玄武岩质)的体系来说,通常为几天至几年,但对偏酸性(如流纹岩质)且演化程度更高的岩浆体系来说,则可以长达几十年甚至几千年(Costa et al., 2020)。即使是时间相对较长的中酸性岩浆体系,扩散年代学给出的时限依然比通过锆石铀钍(U-Th)定年获得的时间尺度小至少两个数量级。这些时间尺度显著低于传统认识,因此引发了有关岩浆热、冷“存储”的争论(Cooper and Kent, 2014; Barboni et al., 2016)。一种可能的解释是,在偏酸性、喷发间隔较长、且规模较大的岩浆体系(如破火山口式火山 - caldera)中,源自下地壳的岩浆可能多次上涌,并与浅部岩浆发生混合,直到达到喷发的临界条件而最终引发喷发。由此,喷发形成火山岩中的矿物可能经历了复杂的热历史,早期岩浆混合对矿物化学成分的改造“痕迹”,很有可能被后期的岩浆混合事件覆盖了。
2.岩浆上升到喷发的时间尺度:‘瞬时’喷发
除了岩浆混合及滞留过程,扩散年代学还可以应用于探究喷发前岩浆从浅部岩浆房上升至地表这一更短过程的时限。由于浅部岩浆上升至地表这一过程通常仅耗费数小时到数天,探究这一过程的时长需要依靠扩散速度更快,且浓度会在岩浆上升(减压)作用下发生变化的元素或组分。目前已有的方法包括模拟矿物中熔体包裹体(melt inclusion)及半开放包裹体(melt embayment)中水的扩散 (图4),橄榄石及辉石中氢元素的扩散,以及长石及石英中的锂元素扩散,等等。此外,地幔捕掳体中橄榄石及辉石中的氢元素扩散,还被用于推测地幔岩浆快速上升至地表的时长。
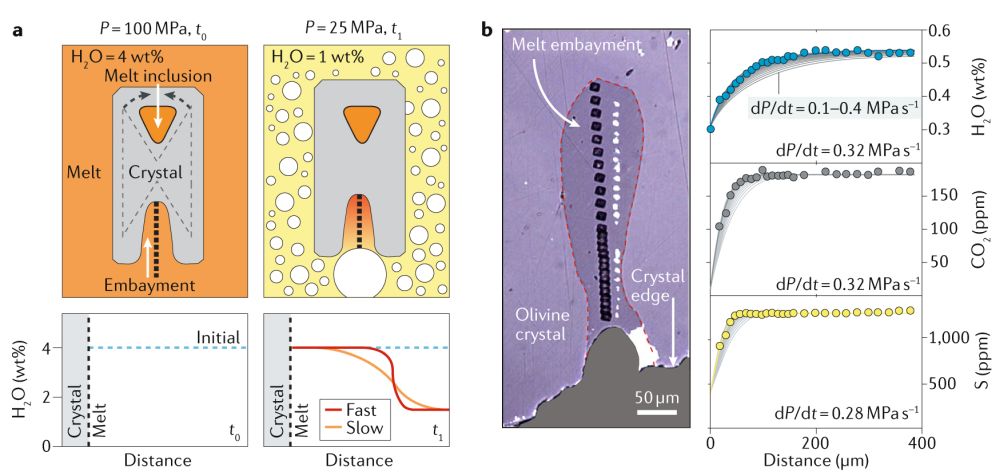
图4 Melt embayment 中H2O扩散反映的岩浆上升时间及减压速率(Costa et al., 2020)
Costa教授团队的李蔚然博士近日发表在EPSL上的文章(Li et al., 2020a)提出,火山岩中磷灰石中的F-Cl-OH元素扩散可以用来约束岩浆上升的时间,并可结合岩浆开始上移的深度估算岩浆上升的速率,从而揭示岩浆上升速率与火山喷发剧烈程度的关系。结合高温扩散实验和实验样品中元素扩散的数值模拟,她们提出磷灰石中F、Cl、OH的扩散遵循“多组分扩散(multicomponent diffusion)”机制,即这三种共存于磷灰石同一晶格位置的阴离子的扩散速度受彼此浓度大小的影响,因此,模拟磷灰石中F-Cl-OH的扩散时间时,需要同时拟合三个组分的浓度剖面。在岩浆上升过程中,岩浆中的水含量会在达到饱和后随减压过程大幅度减小,而岩浆中F和Cl的含量在未达到饱和(即低于其相应溶解度)的情况下会随着微晶的结晶而升高。在岩浆中Cl/OH和F/OH比例升高的情况下,与岩浆接触的磷灰石晶体的边缘则会形成富Cl和/或F,且贫OH的环带,并逐渐向晶体中心扩散。因此,磷灰石晶体边缘F-Cl-OH的扩散时间大致对应了岩浆从开始上升(丢失水)到喷出地表的这段时间。
基于这一理论,Li et al. (2020a)建立了模拟磷灰石中F-Cl-OH三组分扩散的模型,并应用于印度尼西亚默拉皮火山2006年和2010年两次喷发形成的自然样品上(Li et al., 2020b)。这两次喷发的喷发形式和规模有很大差异:2006年为溢流式喷发(VEI 1)而2010年为爆发式、规模更大的喷发(VEI 4),但两次喷发形成的磷灰石包裹体及熔体包裹体反映的喷发前岩浆中挥发分的饱和深度,均在距地表1-10公里范围内。然而,两次喷发形成的火山岩基质中的磷灰石具有明显的成分差异:2006年喷出的基质磷灰石的晶体边缘大多有3-7微米宽的氯元素环带 (图5 a、图5b),而2010年更大规模喷发形成的基质磷灰石没有显著的氯或氟元素环带(图5 c、图5d)。这暗示了2010年喷发前岩浆上升的时间相比2006年更短。Li et al. (2020a)对这些磷灰石晶体中的F-Cl-OH浓度剖面进行了扩散时间的模拟,提出假如两次喷发前岩浆从类似的深度开始上升,那么2010年更大规模的喷发对应的岩浆上升的速度大概比2006年快至少5到10倍。这一发现与“较快岩浆上升通常对应更剧烈的火山喷发”的普遍规律吻合。

图5 印尼默拉皮火山2006年(a,b)和2010年 (c,d) 两次喷发形成的火山岩基质中的磷灰石晶体的挥发分成分。其中,2006年喷出的磷灰石晶体有氯元素环带,而2010年喷出的磷灰石没有显著环带(Li et al., 2020b)
二、扩散年代学——研究展望
扩散年代学在岩浆体系研究中具有广阔的应用前景。通过对比记录在同一岩浆体系中不同矿物中的扩散时间,并结合放射性同位素定年,以及岩浆的地球化学信息,可以更全面地还原岩浆的化学成分随时间和空间的演化历史,从而揭示不同形式的火山喷发背后的机制,并为火山喷发的准确预测奠定基础。
另外,为了获得更高精度的扩散时间,未来的扩散研究还应当致力于:(1)准确获取目标元素扩散系数;(2)测定更高精度和空间分辨率的元素/同位素剖面;(3)将二维扩散模型扩展至三维;(4)在模拟过程中考虑扩散边界的浓度随时间的变化等。
【致谢:感谢岩石圈室路凯博士生的修改。】
主要参考文献
Barboni M, Boehnke P, Schmitt A K, et al. Warm storage for arc magmas[J]. Proceedings of the National Academy of Sciences, 2016, 113(49): 13959-13964.(链接)
Cooper K M, Kent A J R. Rapid remobilization of magmatic crystals kept in cold storage[J]. Nature, 2014, 506(7489): 480-483.(链接)
Costa F, Shea T, Ubide T. Diffusion chronometry and the timescales of magmatic processes[J]. Nature Reviews Earth & Environment, 2020, 1(4): 201-214.(链接)
Girona T, Costa F. DIPRA: A user‐friendly program to model multi‐element diffusion in olivine with applications to timescales of magmatic processes[J]. Geochemistry, Geophysics, Geosystems, 2013, 14(2): 422-431.(链接)
Li W, Chakraborty S, Nagashima K, et al. Multicomponent diffusion of F, Cl and OH in apatite with application to magma ascent rates[J]. Earth and Planetary Science Letters, 2020, 550: 116545.(链接)
Li W, Costa F, Nagashima K. Apatite crystals reveal melt volatile budgets and magma storage depths at Merapi volcano, Indonesia[J]. Journal of Petrology, 2020b: egaa100 .(链接)
Putirka K D. Thermometers and barometers for volcanic systems[J]. Reviews in Mineralogy and Geochemistry, 2008, 69(1): 61-120.(链接)
(撰稿:李蔚然/新加坡地球观测研究所, 李扬/岩石圈室)

