报告人:陈晓非∣整理:方媛媛,李超(地球与行星室)
|
摘要:第一部分关于多阶面波频散曲线提取与结构成像反演,强调了面波反演方法中高阶面波的重要性,提出了频率-矢量波数域变换法(frequency-vector wavenumber transform method,F-J method))来提取多阶面波信息,该方法较传统方法可以更准确地提取面波高阶频散曲线。将高阶频散信息加入面波成像反演中,可以增加反演约束,从而降低反演的不确定性,有效提高面波反演的精度。第二部分关于地震破裂相图和临界震级,陈晓非团队经系统计算给出了地震破裂相图,发现并命名了一种新的破裂类型——自停止破裂(self-arresting rupture),进而确定地震临界震级,为认识地震活动规律和地震破裂过程研究提供了理论基础,可以用来解释许多地震学中的难题。 |
一、多阶面波频散曲线提取与结构成像反演
1. 引 言
地震面波成像方法是地球内部结构成像的重要方法之一。20世纪50年代至70年代,面波成像方法非常活跃,是重要的成像手段;80-90年代,面波成像方法关注度有所衰减,原因是天然地震事件周期长、频率低,导致面波成像结构的分辨率很难提高。过去十多年来得益于背景噪声成像方法的发展,使得面波成像可以向高频、短周期方向发展,所以面波成像又再一次活跃起来。
面波成像最关键的步骤是提取频散曲线,频散曲线是一系列不同频率成分、不同速度的连线,频散曲线与介质模型一一对应,且是非线性关系。所以测得频散曲线,就可以进行反演,进而得到地下的结构信息。确定频散曲线最常用的方法是双台法,根据面波经过两个台站时的时间和距离,就可以求出面波经过这两个台站的速度。利用窄带滤波,分别滤得不同频率成分的面波,就可以求出不同频率成分的速度,进而可以得到频散曲线。由于在实际天然地震资料中,基阶面波与多阶面波混杂在一起,而基阶面波能量较强,所以用传统的双台法很难求得多阶面波成分。除双台法外,利用阵列方法可以得到一部分多阶,但比较模糊。
背景噪声成像方法,可以从噪声中提取出面波,通过对获取的噪声信息进行相关、叠加,便可以获取包含有面波信息的经验格林函数。然后利用测量频散曲线的双台法等方法,便可以获取背景噪声中的频散曲线。相比于天然地震资料,背景噪声获取的频散曲线,频率更高,周期更短,可以获得更精细的结构。
2. 面波反演方法(包括背景噪声反演方法)中高阶面波的重要性
在传统面波反演方法中,一般只利用到面波的基阶成分,但是面波中不光存在基阶,还有高阶成分。仅利用基阶面波成像,反演的结构存在很大的不确定性,需要增加其他的约束来减小反演的非唯一性。如果将面波的高阶信息加入反演,这种反演的不确定性就可以极大地降低(图1)。只有采用基阶、高阶频散曲线联合反演,面波方法才能提供独立、高质量的地球内部结构。
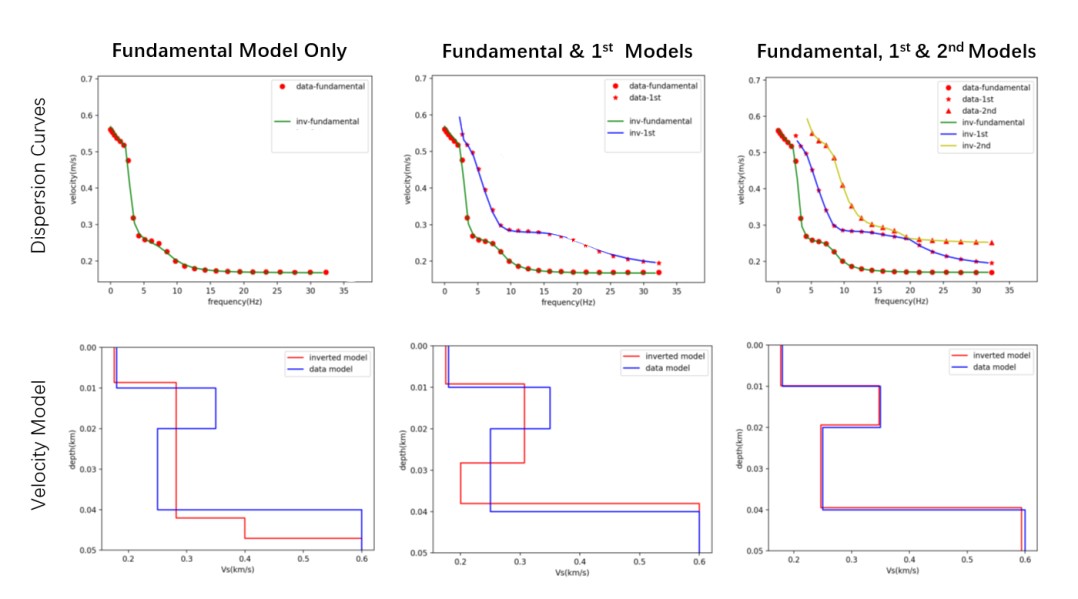
图1 基阶面波反演与多阶面波反演结果对比图
3. 高阶面波频散曲线的提取
既然多阶面波反演如此重要,那么为什么以往不做多阶面波反演呢?因为以往的分析方法当中很难从实际资料中提取到高阶面波信息,基于此,我们开发了一种频率-矢量波数域变换法(frequency-vector wavenumber transform method,F-J 方法)来提取多阶面波信息。
传统的频散曲线提取方法,以双台法为例,是直接根据频散定义,通过窄带滤波,测量两个台站之间面波的到时来提取,对一些高阶面波能量较大的特殊情况,从地震图上可以明显看出来的多阶面波可以提取出来,但通常高阶面波能量小且信噪比低,故不易测量。归根到底是因为在时域中面波的基阶与高阶是混叠在一起的,但是在波数和频率域不同阶的面波是严格区分的,是离散的。所以要想区分出多阶,最好的办法就是将时间-空间域的地震图变换到频率-波数域,即通过傅里叶变换来进行。传统的F-K方法都是基于标量波数变换进行的,而标量波数变换仅对应于二维波动问题,即利用线源对应的平面波的傅里叶变换,但实际问题都是三维的,都是三维波动的传播,因此,此前的F-K方法用于实际数据时都未达到应有的效果。我们的F-J方法利用点源产生的波作为基函数来进行F-K变换,最后可以提取到比较好的多阶面波信息。
首先利用合成地震数据验证该方法的有效性,我们根据已知的地下结构信息,合成了一系列背景噪声信息,然后通过比较利用该方法从噪声信息中提取的频散曲线与通过模型计算出来的频散曲线的拟合程度,发现该方法可以计算出多阶的面波频散曲线,验证了该方法对于理论数据是有效的(图2)。
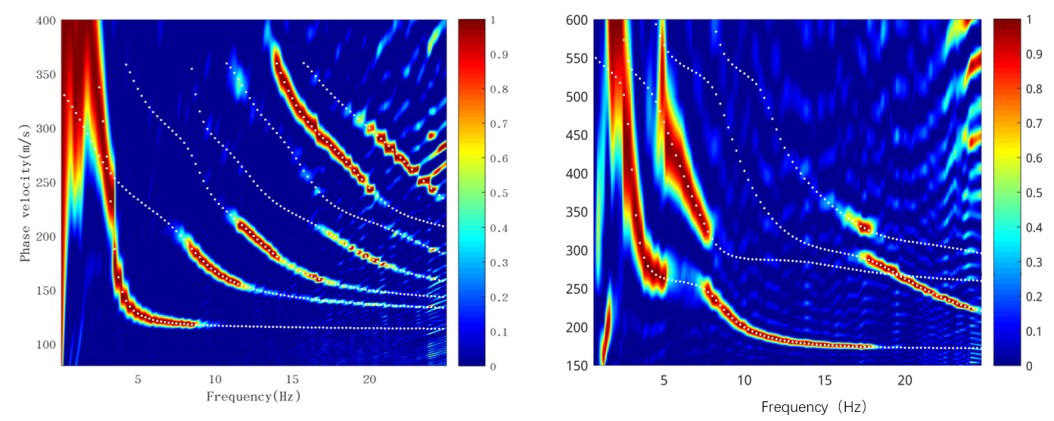
图2 不同理论模型的多阶面波频散曲线提取结果(左:基于模型2的频散曲线;右:基于模型1的频散曲线。具体模型参数可参考Wang et al., 2018)
将该方法利用到实际资料中,利用USArray记录的噪声信息对美国西北部地区、中部地区、中西部地区进行的频散曲线提取,发现该方法都可以比较清晰地提取到面波的多阶信息。另外我们发现,利用上述研究区域的现有模型计算出的频散曲线与通过F-J方法提取出的频散曲线还存在一定差异,说明现有模型还需要进一步改进。我们还将该方法应用于德国地区,利用该地区三组不同时期的地震台站记录的信息分别进行面波频散曲线提取,从结果上看都可以清晰地提取到多阶面波信息,而该地区最新的地下结构模型计算出的频散曲线与我们从实际数据中提取出的频散曲线相比存在系统性的偏低现象,说明模型还有进一步改进的空间。另外该方法也可以应用到海洋地震资料中,同样可以提取多阶面波信息。将该方法利用到华北地区的成像中,如果将山地地区的台站与盆地地区的台站混合在一起提取频散曲线,提取的结果基阶不是很清晰,但如果将山地地区与盆地地区分开做,从山地地区提取的频散曲线非常清晰,而盆地提取的频散曲线非常不好,说明盆地区的地下结构非常复杂,存在很多非水平的垂向结构,成像效果非常差。我们的方法与现有最好的方法MASW方法(多道面波分析方法)相比,可以提取更多的多阶成分,同时对于数据的质量要求不是特别高(图3)。
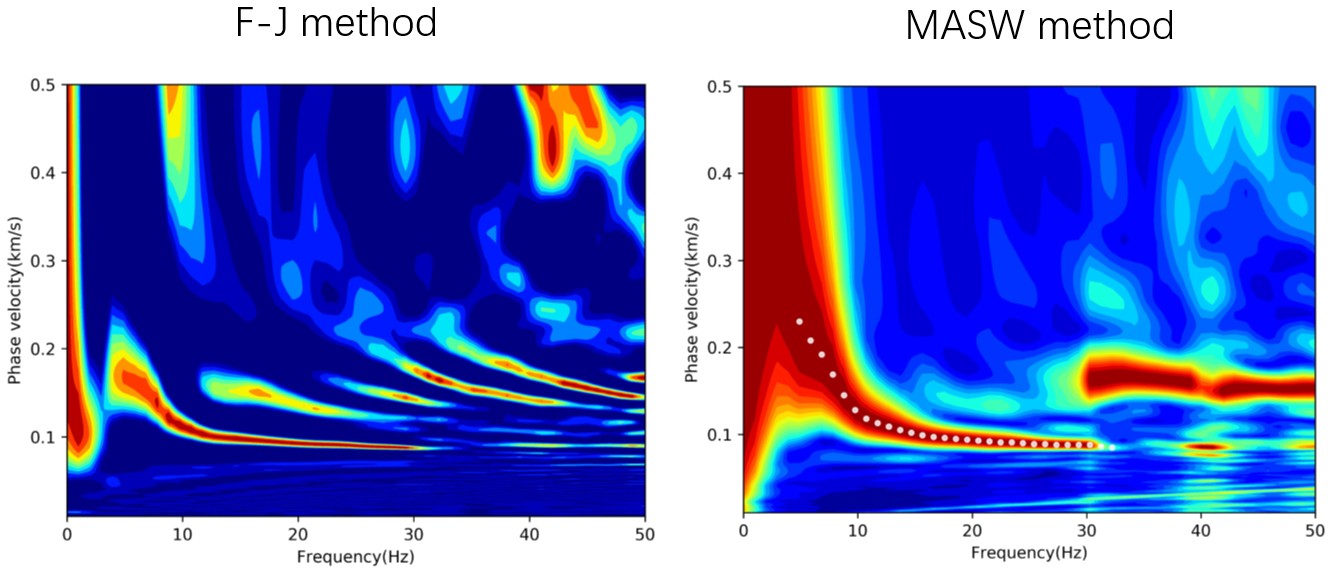
图3 F-J方法与MASW方法对比
4. 利用多阶面波频散曲线反演来改进结构成像
仅利用基阶面波成像,反演结果中没有完全收敛到真实结果,但是将高阶面波成分加入,与基阶成分一起反演,在使用同样的初始模型的情况下,获得的结果不确定性变得更小,更加收敛于真实模型。另外当给定一个更加粗略的初始模型,当加入多阶面波成分,反演结果同样可以收敛到真实模型(图4)。
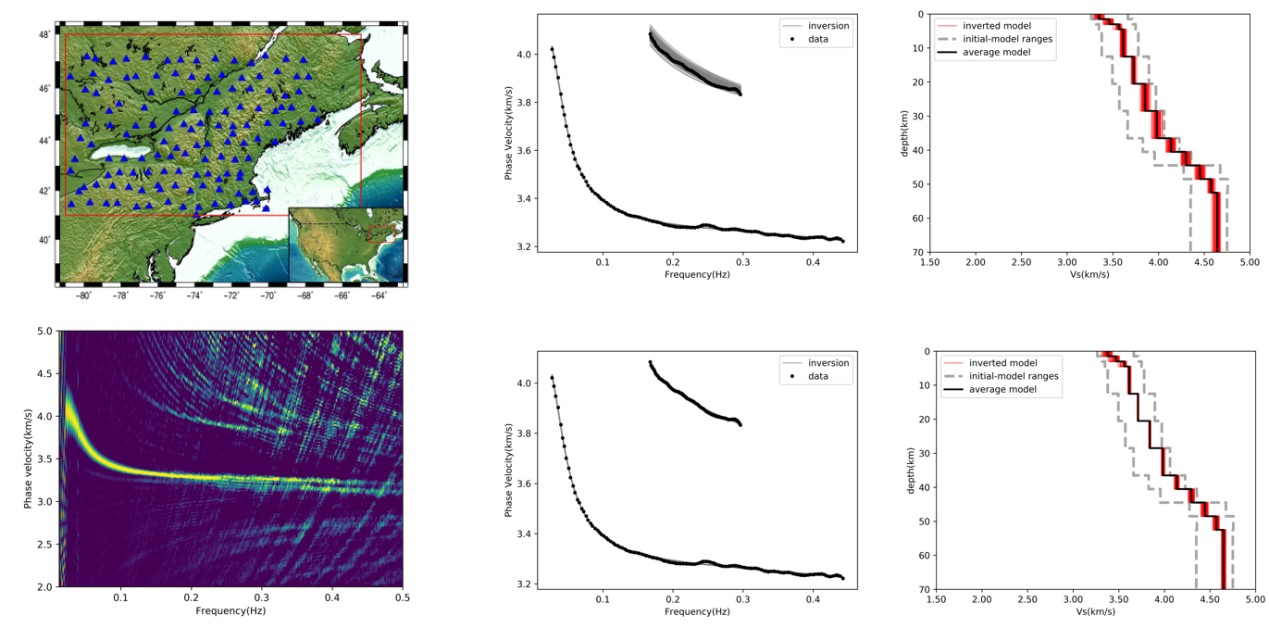
图4 基阶面波反演结果收敛性(上)与多阶面波反演收敛性(下)对比
总之,高阶面波信息对结构反演至关重要。仅仅使用基阶信息的地震面波反演很难成为独立的、高精度的结构成像方法。我们提出的矢量波数变换方法(F-J Method),可以有效提取多阶面波信息。基于F-J Method,我们发展了多阶面波反演方法。这一进展表明:地震面波(主动源、被动源)成像方法,在充分利用多阶频散信息基础上,有望成为一种独立的、具有较高精度的地球内部结构(深、浅)成像方法。
二、地震破裂相图和临界震级
1. 引 言
地震学中最成熟的部分是基于地震波理论的内容,例如地震波成像,因为这些地震学的分支都有成熟的理论基础作支撑。而对于地震本身的动力学过程,缺乏整体的、系统的认识。我们最近对于地震破裂过程的研究,发现了一些新的现象、新的规律,似乎可以为许多地震学中很多看似不相关的、完全不同方向的一些问题提供一个统一的理论基础,这就是接下来要讲到的地震破裂相图。
2. 动力学破裂类型和地震相图
地震本身是个破裂过程,地下内部由于板块构造运动,断层面两侧存在剪切应力的作用和应变的积累。当断层面两侧的应变积累达到一定阈值,超过剪切强度时断层便突然滑动,就发生地震并向外辐射地震波,就有可能造成地面的破坏。
对于地震破裂过程,可以通过弹性动力学方程和断层破裂或滑动准则做一个很好的模拟。从地震开始发生,到地震如何破裂、如何发展、如何停止,所有的过程我们都可以模拟出来。常规的求解地震破裂过程的方法有:有限差分法、谱元法、有限元法、边界元法等等。其中的边界积分方程方法(boundary integral equation method ,BIEM)甚为适合求解这类问题,求解的精度最高,因为这种方法本身最符合描述边值问题。
利用边界积分方程方法,我们发现地震破裂总体而言,存在三种破裂形态:第一种是超剪切破裂(supershear rupture),其破裂速度大于剪切波速度;第二种是亚剪切破裂(sub-rayleigh rupture),其破裂速度始终不超过剪切波速度;第三种我们称之为自停止破裂(self-arresting rupture)。前两种破裂,只要模拟的时间足够长,破裂会一直进行下去,但是对于自停止破裂,破裂传播到一定程度,它就会自己停止。
为了确定这三种破裂的参数范围,我们进行了数值模拟实验。由于计算能力的限制,网格不能无限减小,我们观察随着网格由大逐渐减小时,三种破裂类型之间界限的变化趋势,进而预测出三种破裂类型之间的界限(图5)。
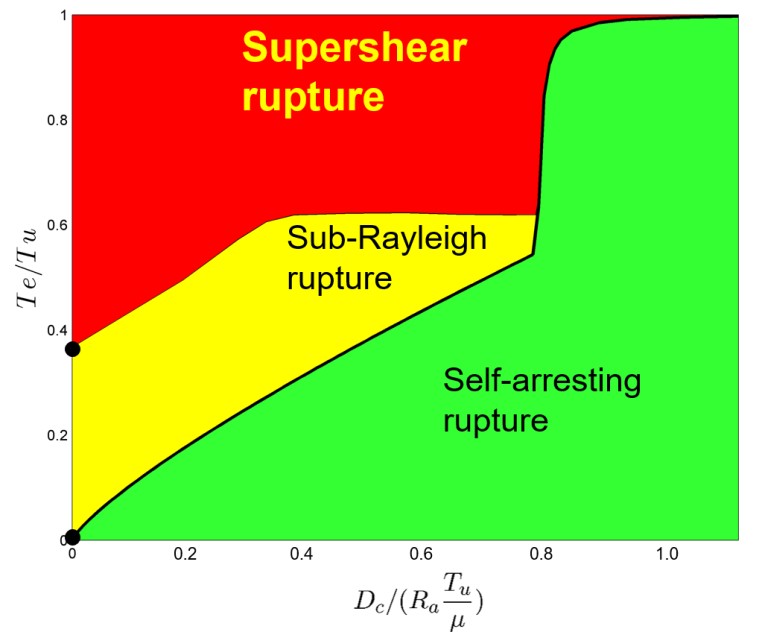
图5 地震破裂相图
上面的地震破裂相图是全空间的情况,我们的工作主要是将全空间的情况发展到半空间,半空间没有简单的格林函数,没有解析解,所以都是数值解,计算量非常大。在半空间的情况下,我们发现,在全空间下的亚剪切破裂全部变成了超剪切破裂,地震破裂相图只存在超剪切破裂和自停止破裂两种状态。为什么亚剪切会变成超剪切呢?这是由于自由地表的作用,我们称之为自由地表诱发的超剪切。以上的结论都是假设断层的埋深为零,当断层埋深不为零时,地震破裂相图介于全空间和半空间相图之间,存在亚剪切破裂区域,但是该区域有所减小,埋深越深,越接近于全空间情况。另外断层角度变化时,地震破裂情况也有所不同,但是对于地震破裂类型没有影响,对于地震能量有影响。
我们的研究也可以对地震灾害防御工作提供借鉴意义,现行的地震预警原理基于:造成地震破坏的地震能量,比如S波,传播速度低于P波波速,P波和S波的到达时间差是地震预警的保障。根据我们的研究,如果地震断层的埋深为零或很浅(<100m),大的走滑型地震一旦失稳破裂,一定会成为超剪切破裂,至少会成为地表诱发超剪切破裂;与亚剪切破裂相比, 超剪切破裂的振幅大,大振幅震相传播速度快(>S波速度, 接近P波速度)且沿断层法向衰减慢。这意味着: 超剪切地震破坏性大(地表震动大、范围广、震动频率高),且破坏性大的震相与P波到时差很小,这将对地震预警造成巨大挑战。
3. 地震破裂相图的发展
早期研究主要发现亚剪切破裂,后来在模拟和实验以及实际资料当中,都发现了超剪切破裂。这两者都是非常清楚的,在我们的计算当中,发现了自停止的破裂。之前,没有人关注自停止破裂,因为过去关于震源动力学模拟的研究都将其当成不成功的数值实验。但是我们坚信这种自停止破裂是符合物理规律的,它是按照弹性力学的物理框架来发展的,对于这种破裂的描述完全是基于数学,没有不合理的地方。所以这种传播到一定程度自己停下来的破裂,也是一种物理结果,是根据我们给定的初值得出的物理结果,不是一个失败的数值模拟实验。
为了验证自停止的破裂到底是不是由地震产生的真实的物理现象,我们依据实际地震进行了模拟研究,给定一系列台站,台站记录到的地震图、地震矩、地震矩速率、破裂谱与实际资料完全符合,因此这就是一个真实的破裂。
过去对于破裂的分类是根据破裂速度和S波速度的差异,如果按照以前的分类方法,我们观察到的破裂现象应该划分为亚剪切破裂,但是这不是这种破裂最本质的特征,它的最本质特征是:随着传播到了一定程度,它会自己停止。超剪切破裂和亚剪切破裂本身不会停止,也就是说如果没有外界的干预,它们会一直破裂下去。因此我们将其命名为自停止的破裂(self-arresting rupture)。
为了研究自停止的破裂的大小,我们做了一系列实验,发现自停止破裂的地震震级可以是3.7、5级甚至是6级,所以这种自破裂的地震是完全有意义的,我们平时多见的很多地震就落在这些震级范围内。
4. 地震临界震级
临界震级的客观定义一直是个未解决的问题。如果我们的地震破裂相图是正确的,我们从逻辑推理就可以确定地震的临界震级。在地震相图上,随着由自停止破裂逐渐向亚剪切破裂接近,地震的震级逐渐增大,地震始终会破裂到一定范围然后停止,但是自停止破裂地震的震级始终存在一个上限值,超过这个上限值,自停止破裂就变成了亚剪切破裂,因此我们可以以这个上限值来定义临界震级。
对于超剪切破裂地震和亚剪切破裂地震,它们只有遇到外部几何、地质特征发生较大变化时,即破裂强度特别大的位置,破裂才会停止。因此对于大地震,其震级依赖于外部环境,而不是初始值。但是对于自停止破裂的地震,其震级大小完全取决于初始值。从某些方面讲,其震级似乎是可预测的,如果可以找到与其相关的基本参数,就可以根据其初始震相,预测其震级,或者给出它的上限。
另一个比较受关注的问题是超剪切破裂的下限是多少?一直以来都无法得到解决,下限是不是6.5?用我们的观点看:超剪切破裂的下限一定不超过自停止破裂的上限,也就是说地震的临界震级就是超剪切破裂的下限。
在理想情况下,如果地震的初始参数是已知的:自停止地震的震级是可以预测的;或者我们可以预测大地震(特征地震)的震级大于临界震级;特征地震的震级可以通过地质调查或者动力学断层模拟估计出来。
5. 小地震的新机制
自停止破裂是小地震的一种机制。小地震和大地震之间差异很大,在某些情况下利用小地震来预测大地震是不成立的。小地震很有可能就是自停止破裂的地震。
根据我们的研究,如果地震是自停止破裂的地震,还没有碰到地质条件突变的位置,它就自己停止了,所以它的谱比较光滑,没有stopping phase(图6上半部分表示自停止破裂的地震)。传统的Crack模型,只有碰到地质条件突变的位置,它才会停止,所以它的谱存在stopping phase(图6下半部分表示传统的Crack模型)。对美国Parkfield地区的实际地震资料分析中,我们也发现了这种规律。依据他人研究低频地震(low-frequency earthquake)给出的震源参数,初步模拟研究表明:仅不破开成核区的自停止破裂能够同时满足低频地震的震源参数。
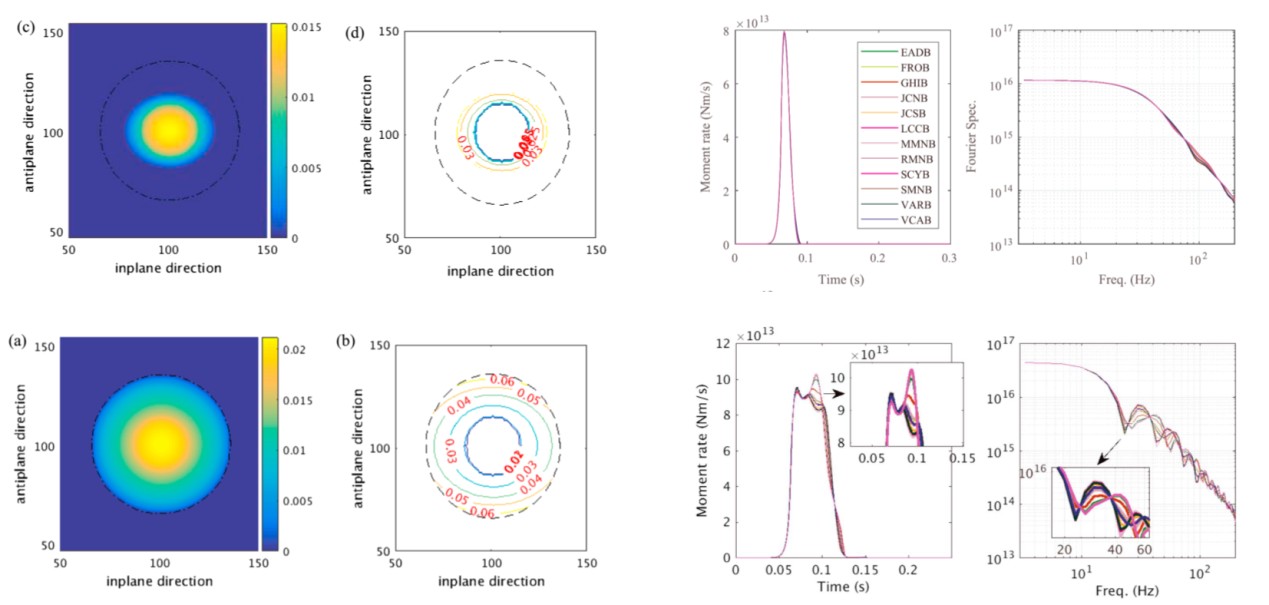
图6 自停止破裂地震与非自停止破裂地震特征对比
根据以上的研究,我们提出的自停止破裂,这是一种新的破裂方式,其最终大小取决于其在理想条件下的成核参数(断层面、破裂空间等)。通过计算自停止破裂的最大震级曲线,我们可以确定地震临界震级。地震破裂相图模型可以解释特征地震模型,并确定超剪切地震的下限。通过对地震相图的研究,我们发现地震学中许多看似互不相关的现象,其实本身都有内在的联系,这种联系的本质还是弹性动力学方程,还是没有跳出物理规律和牛顿力学。也就是说弹性动力学方程不仅可以解释地震波问题,同时也可以解决许多我们过去不理解、不知道如何去做的许多问题。我们的研究基于动力学破裂模拟提供了对地震物理学研究的新观点,许多问题都可以开展进一步的挖掘研究。
以上就是我今天报告的全部内容,谢谢大家!
主要参考文献
Wang J N, Wu G X, Chen X F. Frequency-Bessel transform method for effective imaging of higher‐mode Rayleigh dispersion curves from ambient seismic noise data[J]. Journal of Geophysical Research: Solid Earth, 2019, 124.(原文链接)
Wen J, Chen X, Xu J. A dynamic explanation for the ruptures of repeating earthquakes on the San Andreas Fault at Parkfield [J]. Geophysical Research Letters, 2018, 45(20): 11116-11122.(原文链接)
Xu J, Zhang H, Chen X. Rupture phase diagrams for a planar fault in 3-D full-space and half-space [J]. Geophysical Journal International, 2015, 202(3): 2194-2206.(原文链接)
【说明:本次记录基于陈晓非院士的报告发言整理而成,有所删减。感谢陈棋福研究员、郝金来副研究员对本文的修订。】

