地震波走时是地震波的一个重要属性参数，在地震勘探正反演研究和生产实践中有着重要的应用。事实上，很多种对地球内部结构和物质组成进行成像和探测的方法都要用到地震波走时，如用于速度场反演的地震层析成像等。传统的计算地震波走时的方法都是基于水平地表的。然而，地球的表面常常是起伏或是不规则的，且实际的地球物理观测绝大部分是在这些地表崎岖的地方进行的。近年来，在地震数据的采集、处理和解释中，起伏地表问题越来越引起人们的关注。反演中，常常通过把不规则模型扩展为规则模型来处理地形起伏的问题，即在扩充区域上方填充低速介质然后再用结构网格来剖分上述的扩充模型。该方案会在后续的处理中诱发系列问题。因此，研究和发展一种直接对起伏地表观测的地震资料进行反演的方法具有重要意义。作为反演方法的关键因素，起伏地表下地震波走时的计算显得尤为重要。

地质地球所特提斯研究中心构造物理学科组的博士生兰海强和导师张忠杰研究员提出了一种直接求解起伏地表下地震波初至走时的新方法。他们借助于流体力学中的贴体网格（图1）和坐标变换，发展并构建了“平化”策略下（曲线坐标系中）与地形有关的程函方程。该方程避免了经典的程函方程在复杂地形地震探测中的局限性，为地震探测中复杂地形的处理提供了一个可供考虑的全新方案。

与地形有关的地震波程函方程在数学上被视为各向异性的偏微分方程，原有经典的程函方程求解方法已不适用，为此他们有针对性地引入了Lax-Friedrichs快速扫描法来求解与地形有关的程函方程以获取地震波初至走时场。他们利用高阶加权本质非振荡格式在求解守恒率方程的优势，发展了高阶Lax-Friedrichs快速扫描法。该方法进一步提高了地震波初至走时场求解的精度和计算速度，提高了对大尺度复杂地质模型处理与解释的效能（图2、图3）。他们发展的地震波初至走时计算方法在系列理论模型与实际资料处理中取得了显著效果，这为后续研发一套行之有效的、对起伏地表观测的地震数据进行反演的方法奠定了基础。

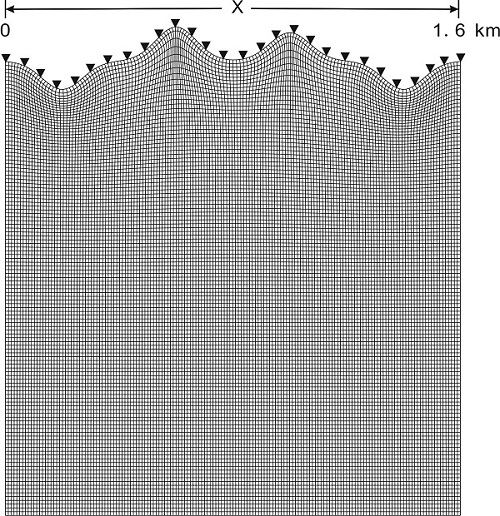
图1　剖分地表起伏模型的贴体网格

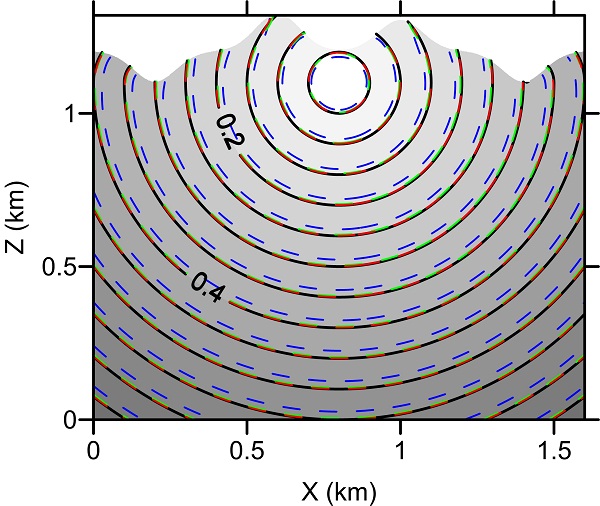
图2　起伏地表下均匀介质中的走时场

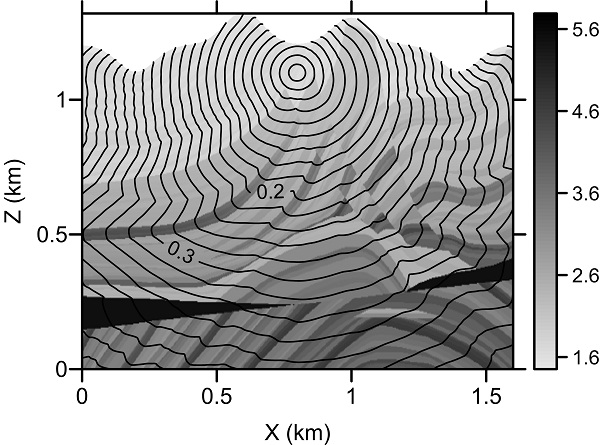
图3　起伏地表下修正的Marmousi模型中的走时场

该研究成果近期发表在国际知名地球物理学科期刊Geophysical Journal International（Lan and Zhang. Topography-dependent eikonal equation and its solver for calculating first-arrival traveltimes with an irregular surface.Geophysical Journal International, 2013, 193: 1010-1026）和Bulletin of the Seismological Society of America（Lan and Zhang. A High-Order Fast-Sweeping Scheme for Calculating First-Arrival Travel Times with an Irregular Surface. Bulletin of the Seismological Society of America, 2013, 103(3): 2070-2082）。