地球内部结构探测是地球物理学的重要研究领域。由于地震学方法在探测精度和探测范围等方面的优势，成为地球内部结构探测的重要途径之一。传统的地震学成像方法，如层析成像、接收函数等，层析成像方法依赖于高频近似假设，难以给出高分辨率的速度结构图像；接收函数成像方法基于水平层状假定，对于存在横向间断面的复杂构造形态较难准确成像。全波形反演方法是利用全波形信息构建高精度速度模型的深部结构成像方法。传统的全波形反演直接匹配观测数据与模拟数据的振幅（L2范数），该方法仅能克服高斯随机噪音。在实际资料中，（1）精确的震源强度较难以估计；（2）波动方程模拟算子难以精确描述实际的地震波传播规律；（3）非高斯噪音、固有干扰等因素，均导致观测数据与模拟数据的直接振幅匹配不够理想。为此，在实际资料处理中，需要一种更加稳健的全波形反演。传统的稳健全波形反演方法——基于Huber范数的全波形反演方法，能够克服高斯随机噪音和非高斯噪音。由于Huber范数涉及到L1范数与L2范数的过渡，而控制该过渡的过渡因子对反演结果非常敏感，为了获取较好的反演结果则需要大量的参数调制。 

　　为此，中国科学院地质与地球物理研究所刘有山博士后和徐涛研究员等人采用归一化零延迟互相关函数作为全波形反演的目标函数，该目标函数松弛了振幅匹配而强调相位约束，它相当于时间域的相位反演，对观测数据和模拟数据中的振幅差异不敏感。因而，基于归一化零延迟互相关函数的全波形反演可以避免精确的震源强度估计，能够直接应用于存在任意（观测数据与模拟数据）振幅差异的数据集而无需振幅均衡校正。相比于传统L2范数全波形反演方法，该方法能够容忍震源时间函数的振幅误差。在噪音的敏感度方面，该方法比Huber范数更加稳健，能够克服高斯噪音和非高斯噪音。相比于Huber函数，归一化零延迟互相关函数不涉及任何参数调制问题，因此它是一种可供选择的稳健全波形反演方法。 

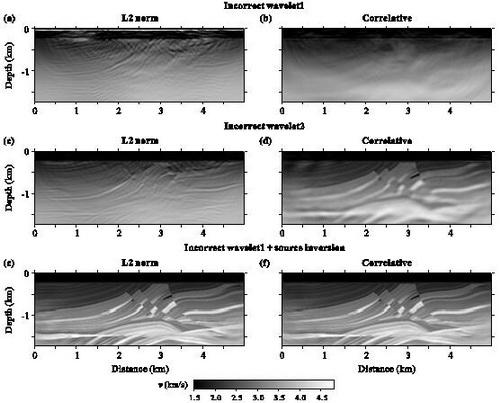
　　图1 不同范数对震源时间函数的敏感度测试
　　第一行：初始震源时间函数存在较大振幅误差的反演结果（无震源时间函数反演）；
第二行：初始震源时间函数存在较小振幅误差的反演结果（无震源时间函数反演）；
第三行：初始震源时间函数存在较大误差+震源时间函数估计；
第一列为传统L2范数的反演结果，第二列为归一化互相关目标函数的反演结果