全波形反演方法是高精度的地震波成像方法。在数学上，它作为一个高度非线性的最优化问题，诸多因素（如反演方法、优化步长等）影响其高效求解。 

　　中国科学院地质与地球物理研究所刘有山博士后和徐涛研究员等人重点研究了非线性共轭梯度法和优化步长对时间域全波形反演的影响:（1）用复杂模型（Marmousi模型）对目前常用的8种非线性共轭梯度法的效率和反演精度（HS，FR，PRP，CD，LS，DY，HZ，HZ1）进行了系统地对比研究。结果表明：在无噪音和高斯白噪声数值试验中，HS，CD，PRP型非线性共轭梯度法均为较高效的方法；DY型非线性共轭梯度法为最不精确的方法，它往往过度估计模型的深部区域。（2）将三种高效的步长优化公式，即直接法、抛物搜索法和两点二次插值法应用于时间域全波形反演中，分别在复杂模型、简单模型、无噪音数据和高斯白噪声数据中对其性能（效率和反演精度）进行了系统的调查研究。 

　　数值试验表明：总体上三种优化步长对高斯白噪声和模型的复杂程度不敏感；对于无噪声（高信噪比）数据，两点二次插值法是最高效的优化步长公式；对于高斯白噪声数据，直接法相对高效；抛物搜索法的收敛速度较慢、效率相对较低。当初始模型偏离真实速度模型较远或者数据被严重的噪音污染时，基于直接法和两点二次插值法优化步长的全波形反演的目标函数在迭代初期较为振荡，而采用抛物搜索法的目标函数能一致性地下降。 

　　本项研究对全波形反演在优化方法和优化步长的选择方面具有重要的理论指导意义。 

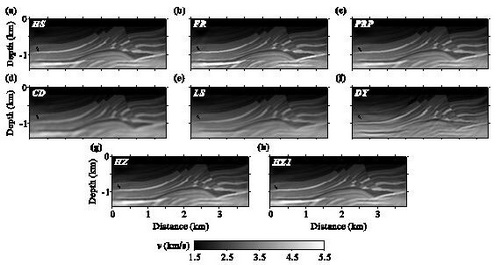
图1 8种非线性共轭梯度法对20高斯白噪音数据的反演结果